-
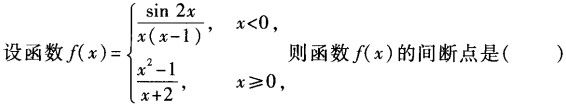
-
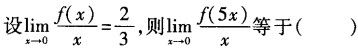
-
下列定积分的值等于0的是().
-
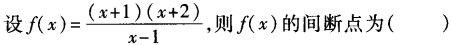
-
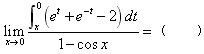
-
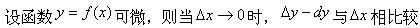
-
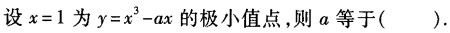
-
设100件产品中有次品4件,从中任取5件的不可能事件是().
-

-
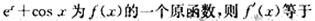
-
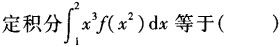
-
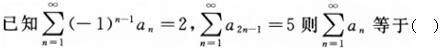
-
下列函数相等的是
-
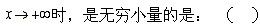
-
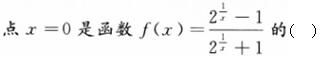
-
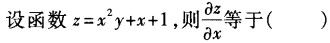
-
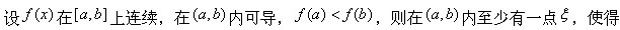
-

-
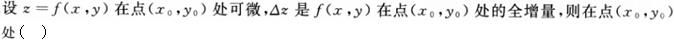
-
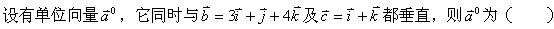
-
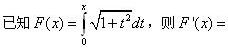
-
设事件A,B的P(B)=0.5,P(AB)=0.4,则在事件B发生的条件下,事件A发生的条件概率P(A|B)=().
-
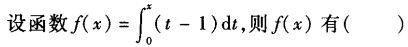
-
-
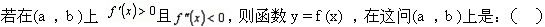
-
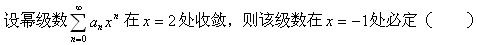
-
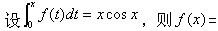
-

-
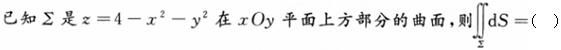
-
函数y=f(x)在点xo处的左、右极限存在且相等是函数在该点极限存在的().
-
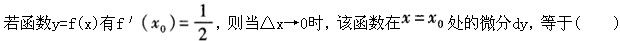
-
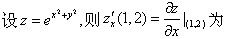
-
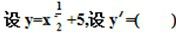
-
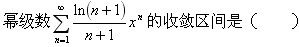
-
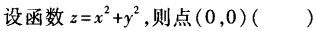
-
-
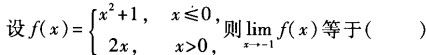
-
-
-
-
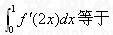
-
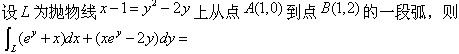
-
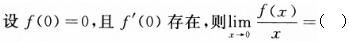
-
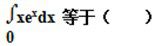
-
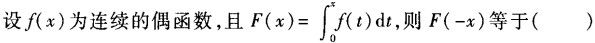
-
-
-
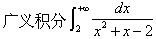
-
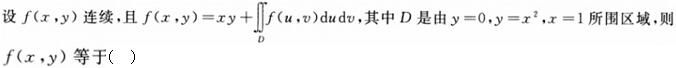
-
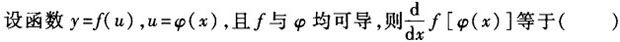
-
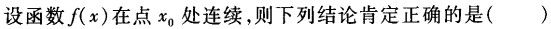
-
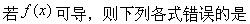
-
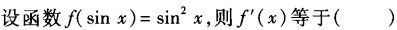
-
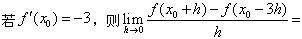
-
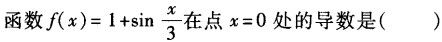
-
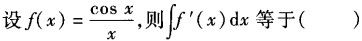
-
下面等式正确的是
-
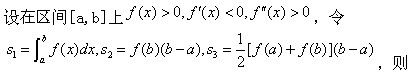
-
-
-
-
下列积分不为0的是
-
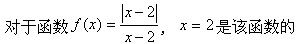
-
-
-
-
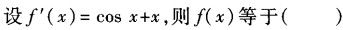
-
-
-
-
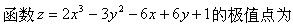
-
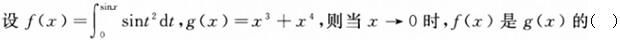
-
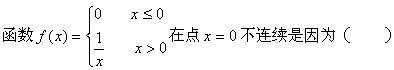
-

-
-
袋中有8个乒乓球,其中5个白色球,3个黄色球,从中一次任取2个乒乓球,则取出的2个球均为白色球的概率为
-
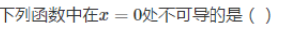
-
设f(x)的一个原函数是xlnx,则f(x)的导函数是
-
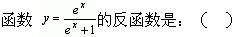
-
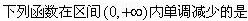
-
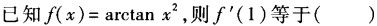
-
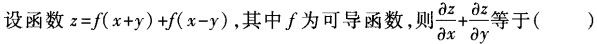
-
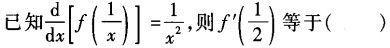
-

-
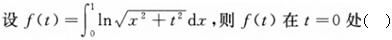
-
若事件A与B互斥,且P(A)=0.5,P(AUB)=0.8,则P(B)等于()
-

-
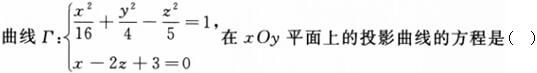
-
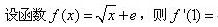
-
-
-
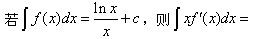
-

-
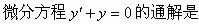
-
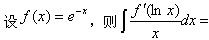
-
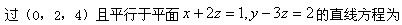
-
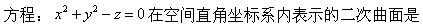
-
-
-
-
-
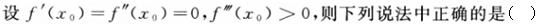
-
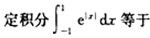
-
下面哪个函数在其定义域内不连续()。
-
-
-
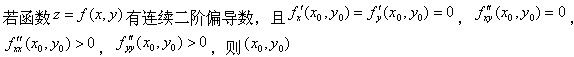
-
-
-
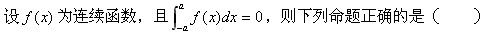
-
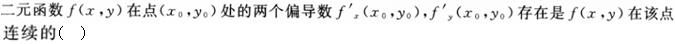
-
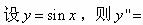
-
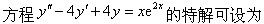
-
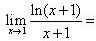
-
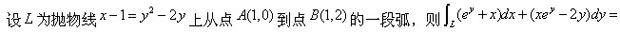
-
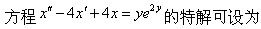
-
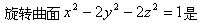
-
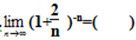
-
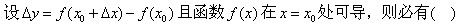
-
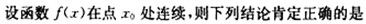
-
下列式子中成立的是
-
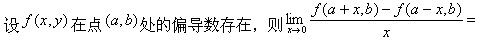
-

-
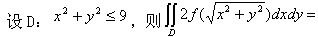
-
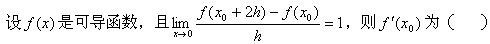
-
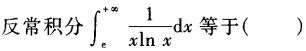
-
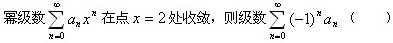
-
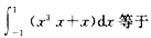
-

-
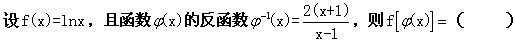
-
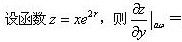
-
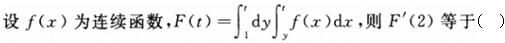
-
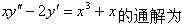
-
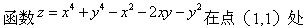
-
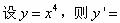
-
在下列函数中,当x→0时,函数f(x)的极限存在的是
-
下列定积分中,其值为零的是()
-
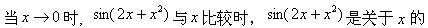
-
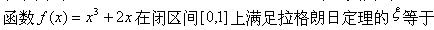
-
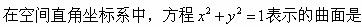
-
-
-
-
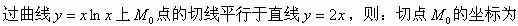
-
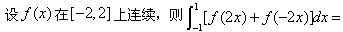
-
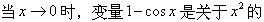
-
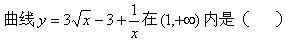
-
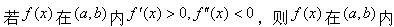
-
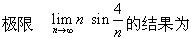
-
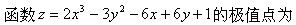
-
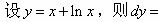
-
若f(x)在点x=a处可导,则f′(a)≠()。
-
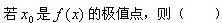
-
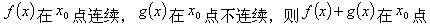
-
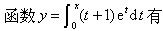
-
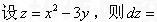
-
下列级数收敛的是
-
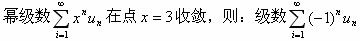
-
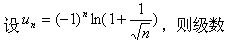
-
-
-
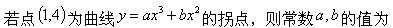
-

-
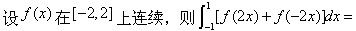
-
设f(x)=xsinx+cosx,则下列命题中正确的是()。
-
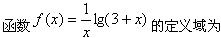
-
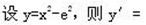
-
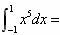
-
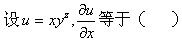
-
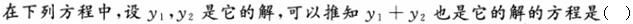
-
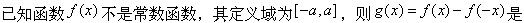
-
当x→0时,下列哪一个无穷小是x的三阶无穷小。()
-
当x→0时,下列结论正确的是
-
下列反常积分发散的是()。
-
若a·b=a·c,则()。
-
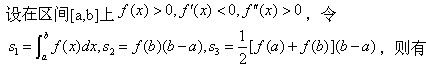
-
-

-
-
下列广义积分收敛的是
-
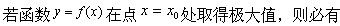
-
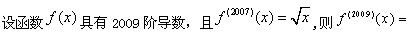
-
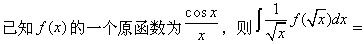
-
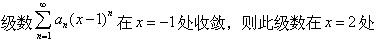
-

-
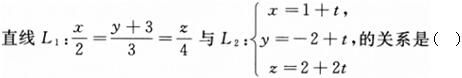
-
下列等式中正确的是
-
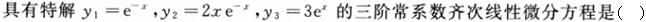
-
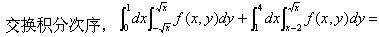
-
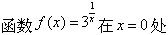
-
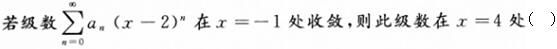
-
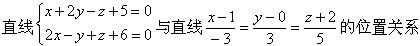
-
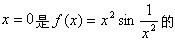
-
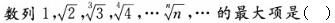
-
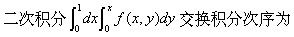
-
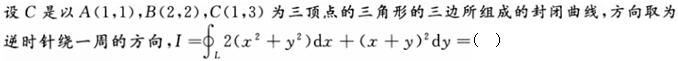
-
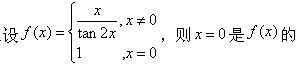
-
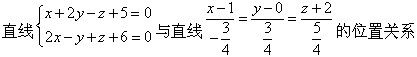
-
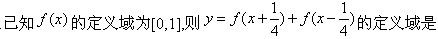
-
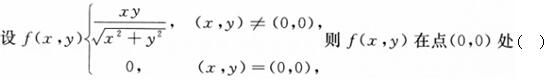
-
下列解中是某二阶常微分方程的通解为
-
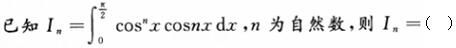
-
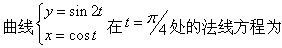
-
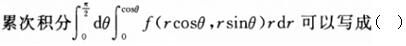
-
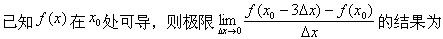
-
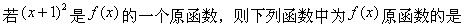
-
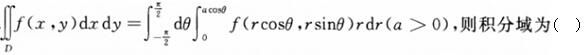
-
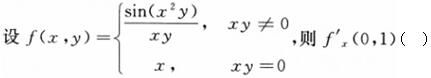
-
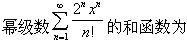
-
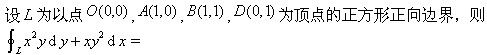
-
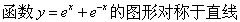
-
下列级数中,收敛的有
-
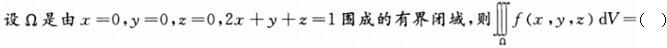
-
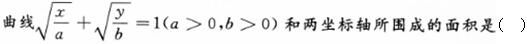
-
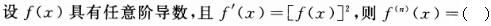
-
函数厂(x)具有连续的二阶导数,且f″(0)≠0,则x=0()。
-
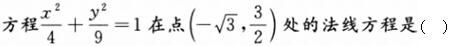
-
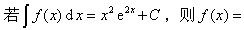
-
空间点P(1,3,-4)关于平面3x+y-2z=0的对称点是()。
-
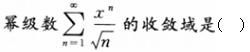
-

-

-
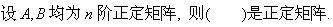
-

-
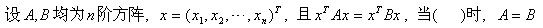
-
设A是n阶方阵,则|A|=0的必要条件是().
-
矩阵A()时可能改变其秩.
-
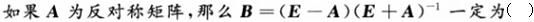
-
设A、B都是n阶非零矩阵,且AB=0,则A和B的秩
-

-
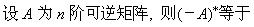
-
若向量组α,β,γ线性无关,α,β,σ线性相关,则()。
-

-

-
下列矩阵为正定的是
-
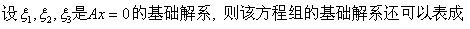
-

-
下列矩阵中,()不是初等矩阵。
-

-
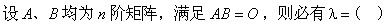
-
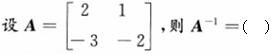
-
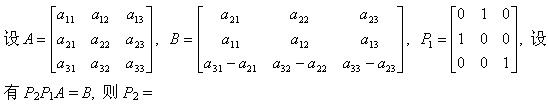
-
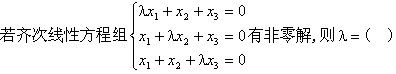
-
设A、B为同阶可逆矩阵,则
-
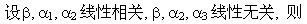
-
设A,B是n阶方阵,A≠0且AB=0,则().
-
设A,B是n阶方阵,且秩A=秩B,则
-
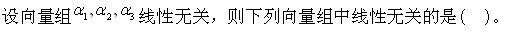
-
设a为N阶可逆矩阵,则().
-
下列矩阵中A与B合同的是()。
-
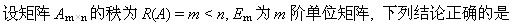
-
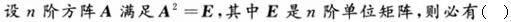
-
下列二次型中正定二次型是()。
-
设A、B都是n阶方阵,下面结论正确的是
-
零为矩阵A的特征值是A为不可逆的
-
与n阶单位矩阵E相似的矩阵是
-
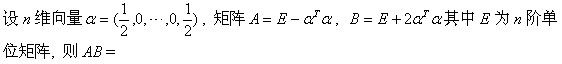
-

-
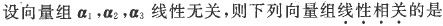
-

-

-
若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则()
-
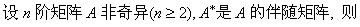
-
设A为m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r1,矩阵B=AC的秩为r,则
-
若方阵A与B相似,则有().
-
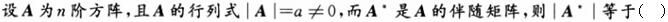
-
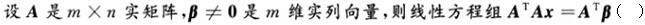
-
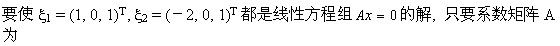
-
下列n阶行列式,一定等于-1的是()。
-
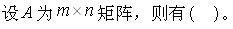
-
设A和B均为n阶矩阵,则必有()。
-
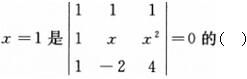
-
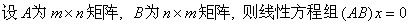
-
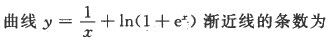
-
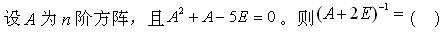
-
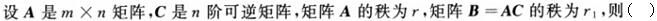
-

-
设A为n阶方阵,则以下结论正确的是()。
-
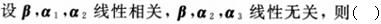
-

-
下列矩阵中不能相似对角化的为()。
-
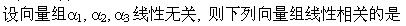
-
设A,B是n(n≥2)阶方阵,则必有().
-
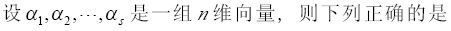
-

-
n阶矩阵A可逆的充分必要条件是
-
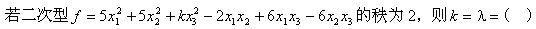
-
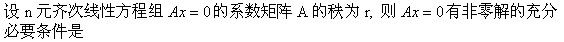
-

-
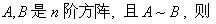
-
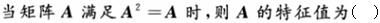
-
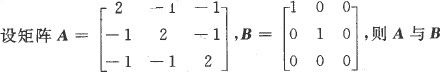
-
下列矩阵中,A和B相似的是()。
-

-
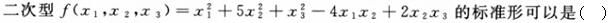
-
设4阶矩阵A与B仅有第3行不同,且|A|=1,|B|=2,则|A+B|=()。
-
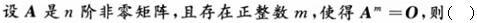
-
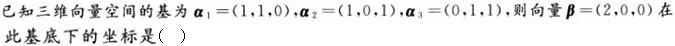
-
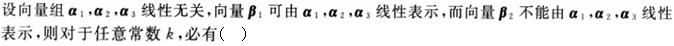
-
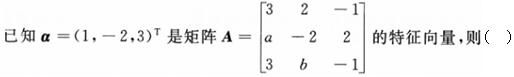
-

-

-
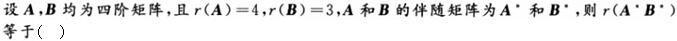
-
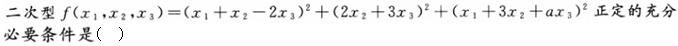
-
-

-

-
-
设A为m×n矩阵,齐次线性方程组Ax=0仅有零解的充要条件是()。
-
-

-
设2n阶行列式D的某一列元素及其余子式都等于a,则D=()。
-

-

-
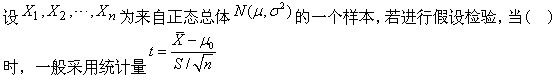
-
当事件A与事件B同时发生时,事件C必发生,则()。
-

-
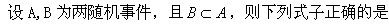
-
-
在对单个正态总体均值的假设检验中,当总体方差已知时,选用()
-
-
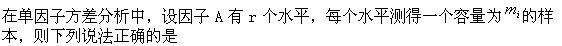
-
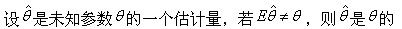
-
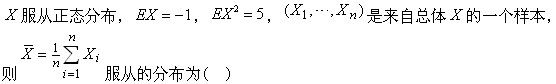
-

-
在一次假设检验中,下列说法正确的是
-
一口袋中有3个红球和2个白球,某人从该口袋中随机摸出一球,摸得红球得5分,摸得白球得2分,则他所得分数的数学期望为()
-
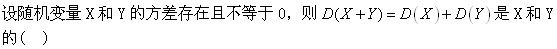
-

-
设随机变量X服从N(0,2),则()。
-
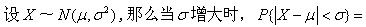
-
设随机变量X服从指数分布,则随机变量Y=min(X,2)的分布函数()。
-
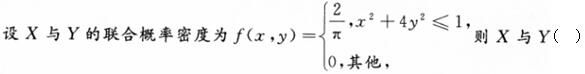
-

-
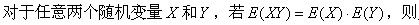
-
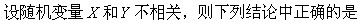
-

-
将一枚硬币重复掷n次,以X和Y分别表示正面向上和反面向上的次数,则X与Y的相关系数等于()。
-
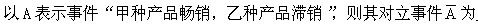
-
-
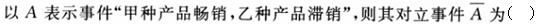
-
投掷两个均匀的骰子,已知点数之和是偶数,则点数之和为6的概率为()
-
-
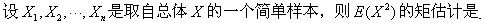
-
对于事件A,B,下列命题正确的是()
-
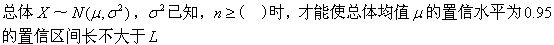
-
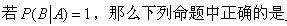
-
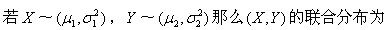
-
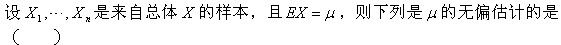
-

-
如果随机事件A,B满足条件0<P(A)<1,P(B)>0,P(B|A)=P(B|A),则下列正确的是()。
-
如果f(x)是某随机变量X的概率密度函数,则可以判断也为概率密度的是()。
-
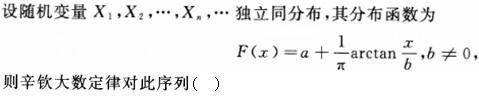
-

-

-
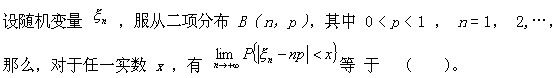
-

-
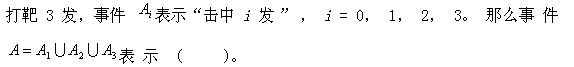
-
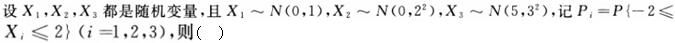
-
下列二无函数中,()可以作为连续型随机变量的联合概率密度。
-
在一个确定的假设检验中,与判断结果相关的因素有()
-
在假设检验问题中,犯第一类错误的概率α的意义是()
-
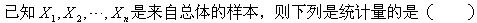
-
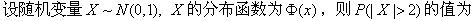
-
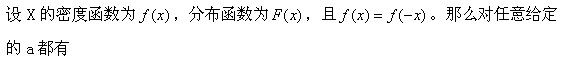
-

-
设随机变量X和Y独立同分布,记U=X-Y,V=X+Y,则随机变量U与V也()。
-
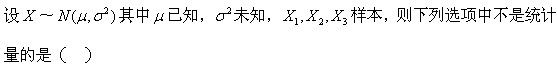
-
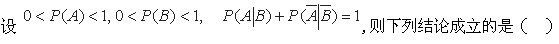
-
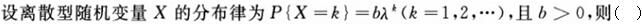
-
从1、2、3、4、5这五个数字中等可能地、有放回地接连抽取两个数字,则这两个数字不相同的概率为()
-

-
下列函数中,可作为某一随机变量的分布函数是()
-

-
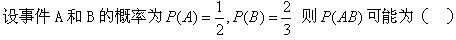
-
袋中有50个乒乓球,其中20个黄的,30个白的,现在两个人不放回地依次从袋中随机各取一球。则第二人取到黄球的概率是()
-
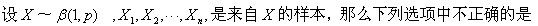
-

-
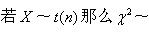
-

-
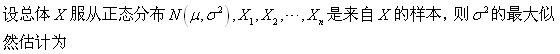
-
假设随机变量X的分布函数为F(x),密度函数为f(x).若X与-X有相同的分布函数,则下列各式中正确的是()
-
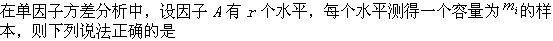
-
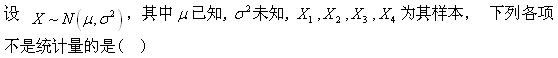
-

-
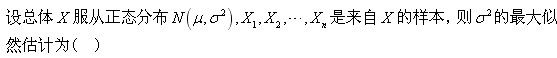
-
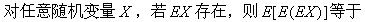
-
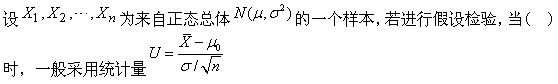
-
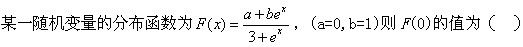
-

-
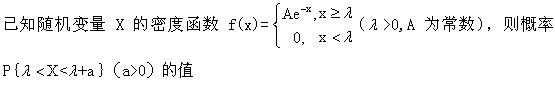
-
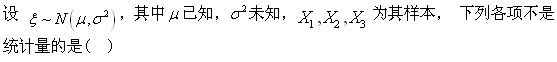
-
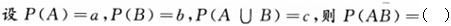
-

-
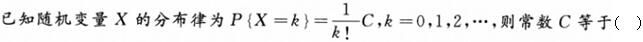
-
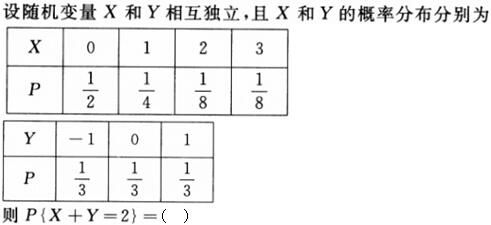
-
设随机事件A与B相互独立,且P(B)=0.5,P(A-B)=0.3,则P(B-A)=()。
-
-
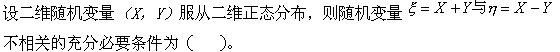
-

-

-

-
战士甲进行射击训练,已知甲每次射击击中10环、9环、8环或8环以下的概率分别为0.2,0.3,0.5。现甲独立射击了2次,则甲至少有1次射中10环的概率是()。
-
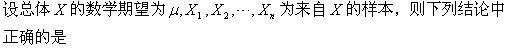
-

-

-
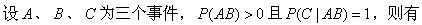
-
在手机号码中,后8位不出现“8”的概率为()。
-
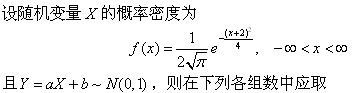
-

-

-
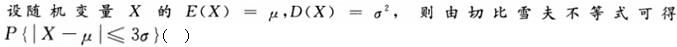
-
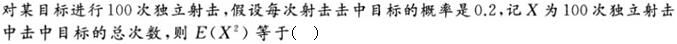
-
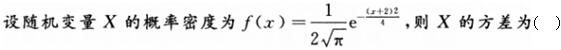
-
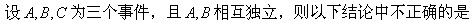
-
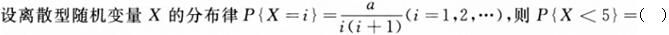
-
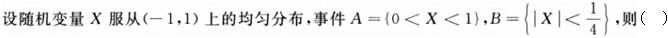
-
如果X与Y满足D(X+Y)=D(X-Y),则必有()。
-
在一次军事演习中,某舟桥连接到命令要赶到某小河D岸为进行中的A部队架设浮桥。假设舟桥连到达D岸的时间服从7点到7点30分这时间段内的均匀分布,架设需要20分钟时间,A部队到达D岸的时间服从7点30分到8点这时间段内的均匀分布。且舟桥连的到达时间和A部队的到达时间相互独立。则A部队到达D岸时能立即过桥的概率是()。
-
-
-
-

-
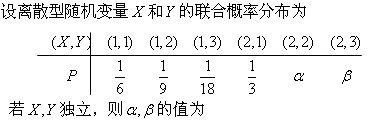
-
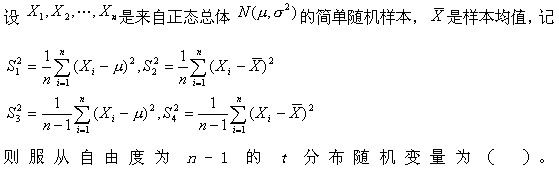
-
已知二维随机变量(X,Y)服从区域[0,1]×[0,1]上的均匀分布,则()。
-
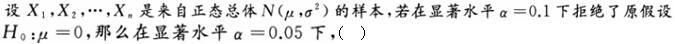
-
同时抛掷三枚质地完全相同的硬币,则正面与反面都出现的概率为()。
-
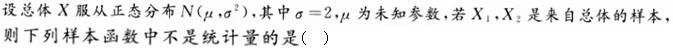
-
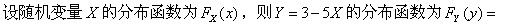
-
设两个互相独立的随机变量X和Y的方差分别为2和4,则随机变量2X-3Y的方差;是()。
-
设某宿舍共有5名士兵,就寝时帽子均统一挂在宿舍内的帽钩上,在连队进行夜间紧急集合训练时,该宿舍的5名士兵随机从帽钩上拿一顶帽子戴上,则正好戴的是自己帽子的平均战士人数为()。
-

-

-
-
-

-
-
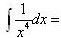
-
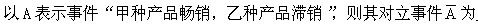
-
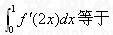
-

-
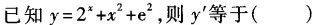
-
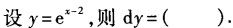
-
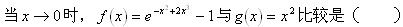
-
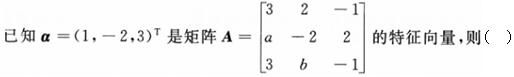
-
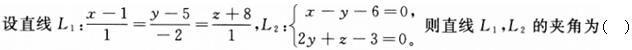
-
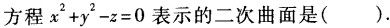
-
设函数f(x)=2sinx,则f′(x)等于().
-
如果X与Y满足D(X+Y)=D(X-Y),则必有()。
-
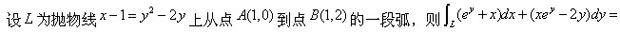
-
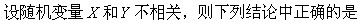
-
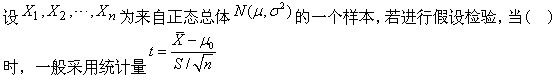
-
-
-
-
-
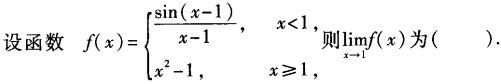
-
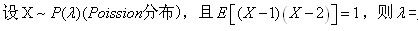
-
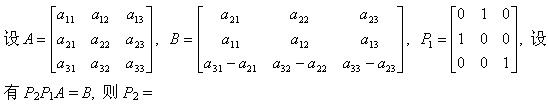
-
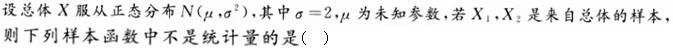
-
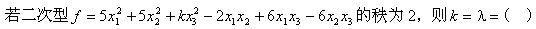
-
微分方程y′+3y=8的通解是()。
-
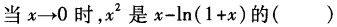
-

-
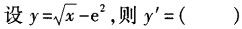
-
下列函数相等的是
-
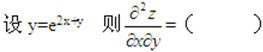
-
若事件A与B互斥,且P(A)=0.5P(AUB)=0.8,则P(B)等于()
-
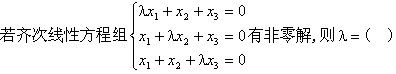
-
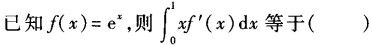
-

-
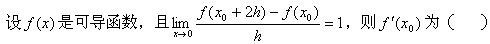
-
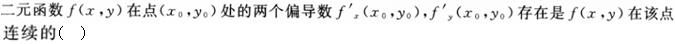
-
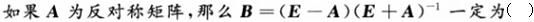
-
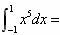
-
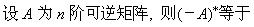
-
设随机变量X和Y独立同分布,记U=X-Y,V=X+Y,则随机变量U与V也()。
-
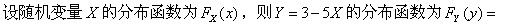
-
下列级数绝对收敛的是
-
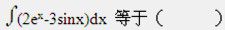
-

-
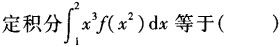
-
一口袋中有3个红球和2个白球,某人从该口袋中随机摸出一球,摸得红球得5分,摸得白球得2分,则他所得分数的数学期望为()
-
下列级数中,收敛的有
-
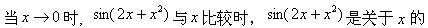
-
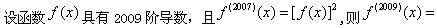
-
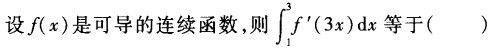
-
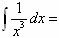
-
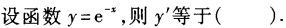
-
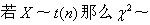
-
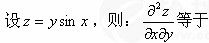
-
与n阶单位矩阵E相似的矩阵是
-
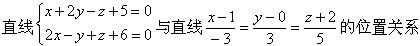
-
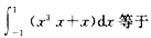
-
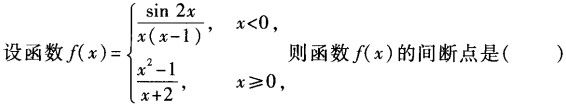
-
当x→0时,下列是无穷小量的是:
-
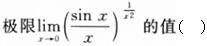
-
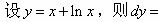
-

-
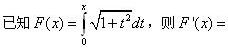
-
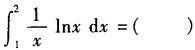
-
曲线y=lnx在点(e,1)处切线的斜率为().
-
微分方程y′+y=0的通解为().
-
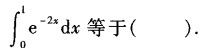
-

-
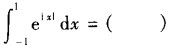
-
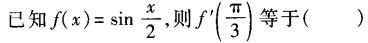
-
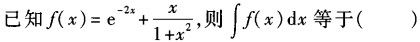
-
下列等式不成立的是().
-
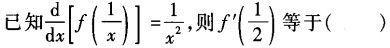
-
设f(x)的一个原函数是xlnx,则f(x)的导函数是
-

-
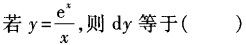
-
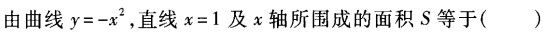
-
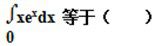
-
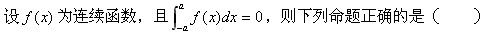
-
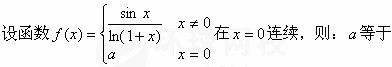
-
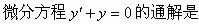
-
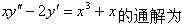
-
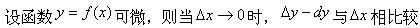
-
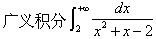
-
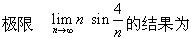
-
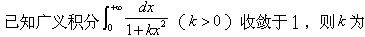
-
下列解中是某二阶常微分方程的通解为
-
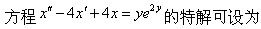
-

-
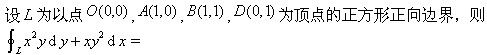
-
若n阶矩阵A,B有共同的特征值,且各有n个线性无关的特征向量,则()
-
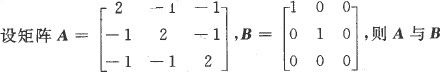
-
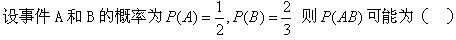
-

-
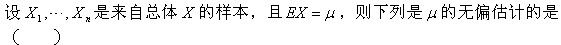
-

-
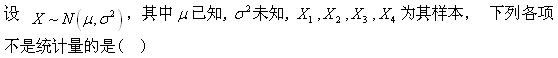
-
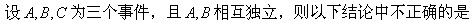
-
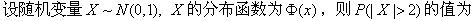
-

-
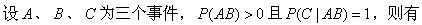
-
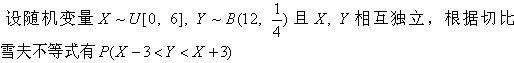
-
当x→0时,下列哪一个无穷小是x的三阶无穷小。()
-
函数厂(x)具有连续的二阶导数,且f″(0)≠0,则x=0()。
-
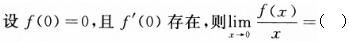
-
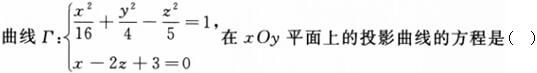
-
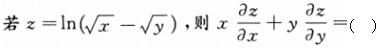
-
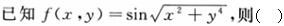
-
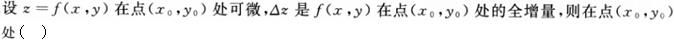
-
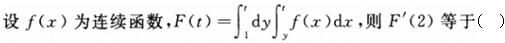
-
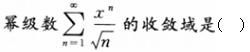
-
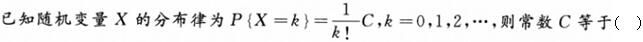
-
如果f(x)是某随机变量X的概率密度函数,则可以判断也为概率密度的是()。
-

-
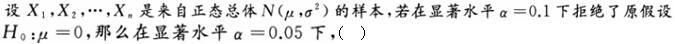
-
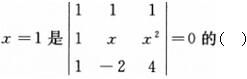
-
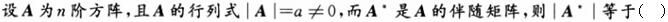
-
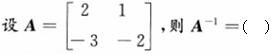
-
设A和B均为n阶矩阵,则必有()。
-
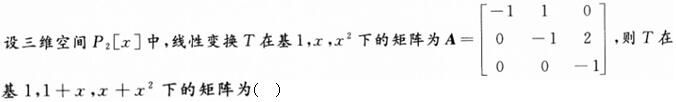
-
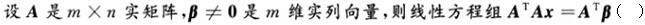
-

-
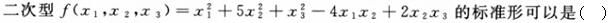
-
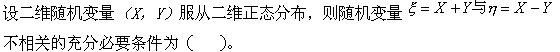
-
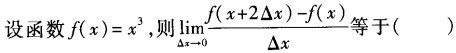
-
下列二无函数中,()可以作为连续型随机变量的联合概率密度。
-
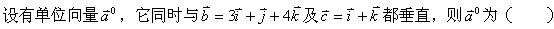
-
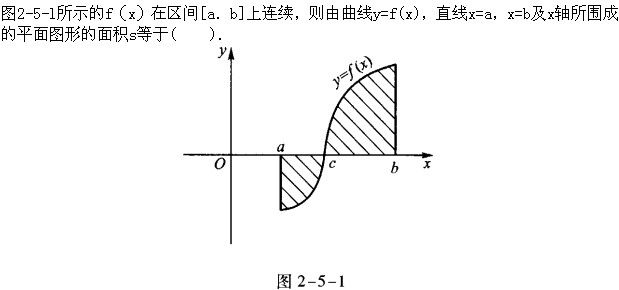
设f(x)为区间[a,b]上的连续函数,则曲线y=f(x)与直线x=a,x=b,y=0所围成的封闭图形的面积为().
-
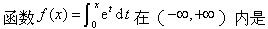
-
n阶矩阵A可逆的充分必要条件是
-
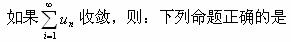
-
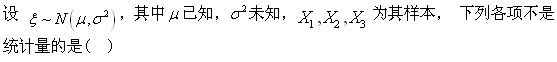
-
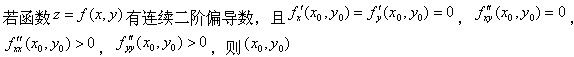
-
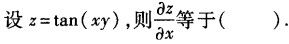
-
设a为N阶可逆矩阵,则().
-
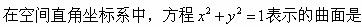
-

-

-
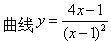
-
若f(x)可导,则下列各式错误的是
-
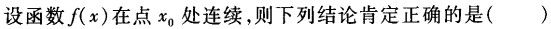
-
下列等式中正确的是
-
如果随机事件A,B满足条件0<P(A)<1,P(B)>0,P(B|A)=P(B|A),则下列正确的是()。
-

-
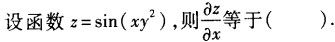
-
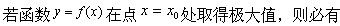
-
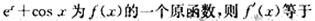
-
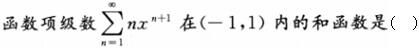
-
设A,B是n阶方阵,A≠0且AB=0,则().
-
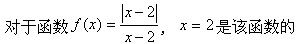
-
若方阵A与B相似,则有().
-

-
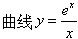
-
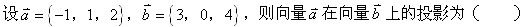
-
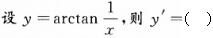
-
设f(x)的一个原函数为xln(x+l),则下列等式成立的是().
-

-
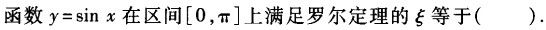
-
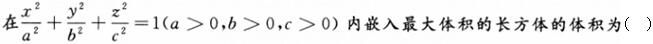
-
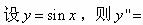
-
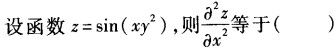
-
设事件A,B的P(B)=0.5,P(AB)=0.4,则在事件B发生的条件下,事件A发生的条件概率P(A|B)=().
-
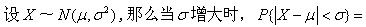
-
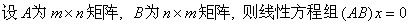
-
下列说法正确的是()。
-
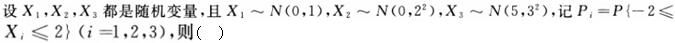
-
对于任意随机变量X和Y,与命题“X和Y不相关”不等价的是()。
-

-
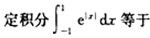
-
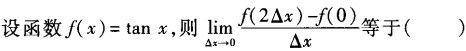
-
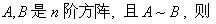
-
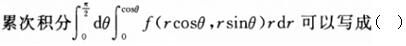
-

-
下面等式正确的是
-
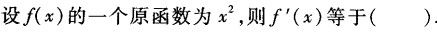
-
下列二次型中正定二次型是()。
-
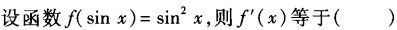
-
下列微分方程中,可分离的变量方程是
-
若cotx是f(x)一个原函数,则f(x)等于()
-
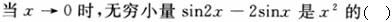
-
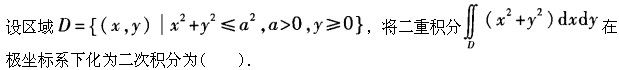
-
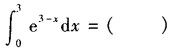
-
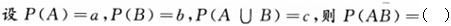
-
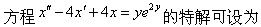
-
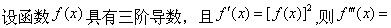
-
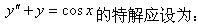
-
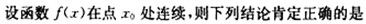
-
袋中有8个乒乓球,其中5个白色球,3个黄色球,从中一次任取2个乒乓球,则取出的2个球均为白色球的概率为
-
矩阵A()时可能改变其秩.
-
设f′(x)=l+x,则f(x)等于().
-
设f(x)的一个原函数为1nx,则f(x)等于().
-
-
设A,B是n(n≥2)阶方阵,则必有().
-
若f(x)在点x=a处可导,则f′(a)≠()。
-
-
-
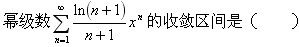
-
下面等式正确的是().
-
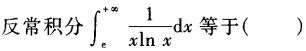
-

-

-
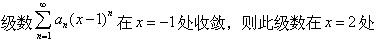
-
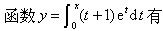
-

-
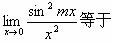
-
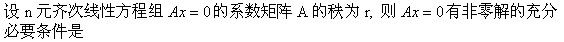
-
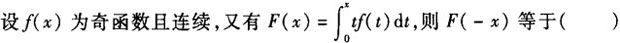
-
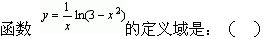
-
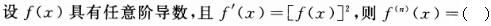
-
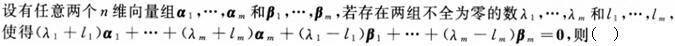
-
函数y=f(x)在(a,6)内二阶可导,且f′(x)>0,f″(x)<0,则曲线y=f(x)在(a,6)内().
-
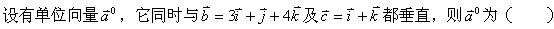
-
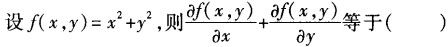
-
函数y=f(x)在点xo处的左、右极限存在且相等是函数在该点极限存在的().
-
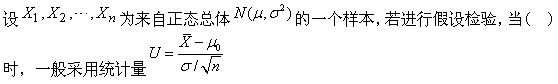
-
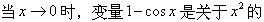
-
-
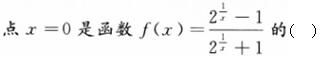
-

-
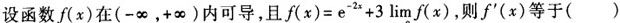
-
-
-
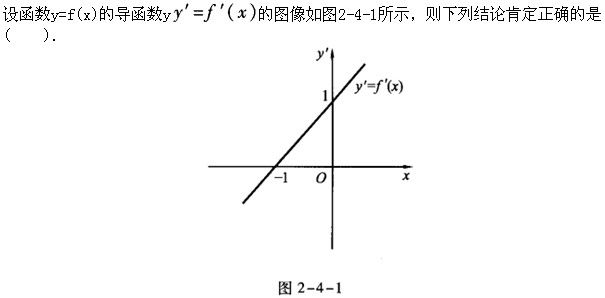
设函数y=f(x)的导函数,满足f′(一1)=0,当x<-l时,f′(x)<0;当x>-l时,f′(x)>0.则下列结论肯定正确的是().
-
-
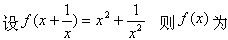
-
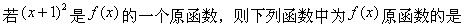
-
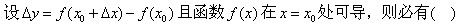
-
下列函数在区间[0,3]上不满足拉格朗日定理条件的是()
-
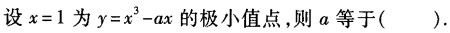
-
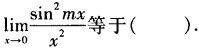
-
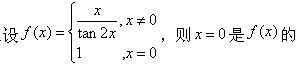
-
设A,B是n阶方阵,且秩A=秩B,则
-
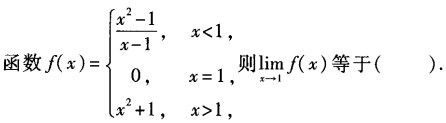
-

-
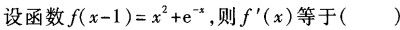
-
下列矩阵中,A和B相似的是()。
-
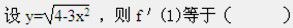
-
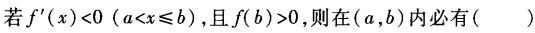
-
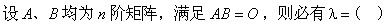
-
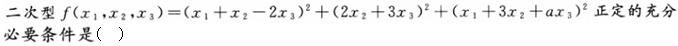
-

-
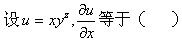
-
-
-
-
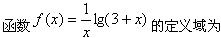
-
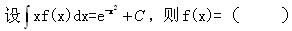
-
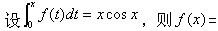
-
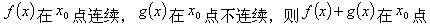
-
在下列函数中,当x→0时,函数f(x)的极限存在的是
-
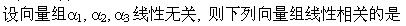
-
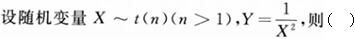
-
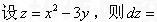
-

-
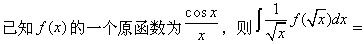
-
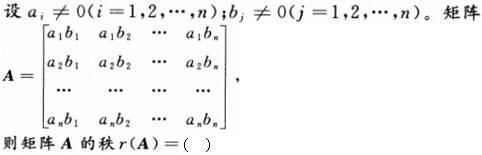
-
设A为n阶方阵,则以下结论正确的是()。
-
-
-
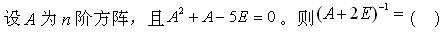
-

-
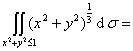
-

-
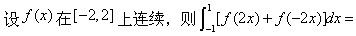
-
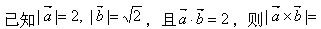
-
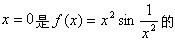
-

-
在一个确定的假设检验中,与判断结果相关的因素有()
-

-
在区间(0,+)内,下列函数中是无界函数的为()
-
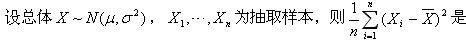
-
-
-
-
空间点P(1,3,-4)关于平面3x+y-2z=0的对称点是()。
-
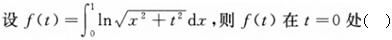
-
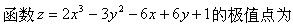
-
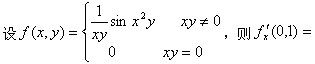
-
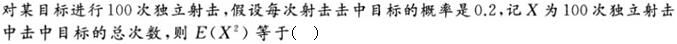
-
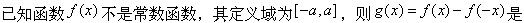
-
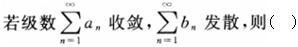
-
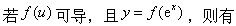
-
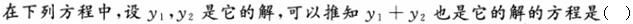
-
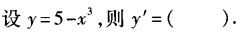
-
-

-
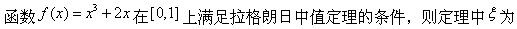
-
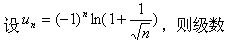
-
下列函数中,可作为某一随机变量的分布函数是()
-
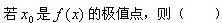
-
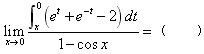
-
-
-
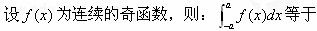
-
下列关系中正确的是
-
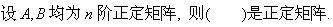
-
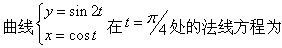
-

-
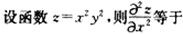
-
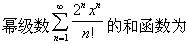
-

-
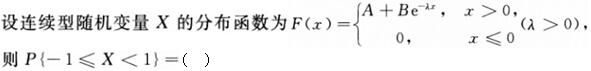
-
设y=x-5,则dy=().
-

-

-
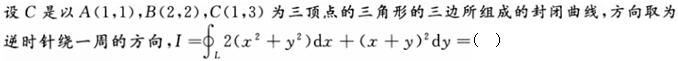
-
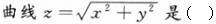
-
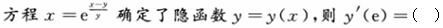
-
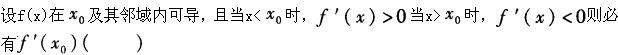
-
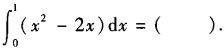
-
设y=f(x)二阶可导,且,f′(1)=0,f″(1)>0,则必有().
-
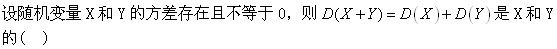
-
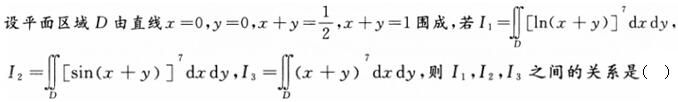
-
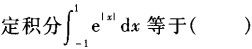
-
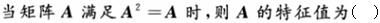
-
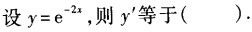
-

-
当x→0时,下列哪一个函数不是无穷大量
-
对于事件A,B,下列命题正确的是()
-

-
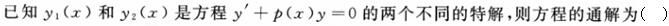
-
-
-
设y=sin(x-2),则dy=().
-

-
-
设f(x)=xsinx+cosx,则下列命题中正确的是()。
-
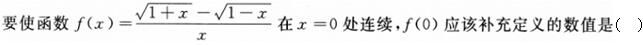
-
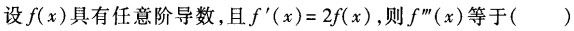
-
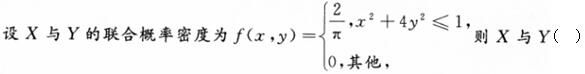
-
设随机变量X服从N(0,2),则()。
-
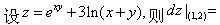
-

-
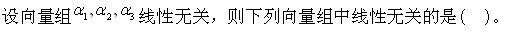
-
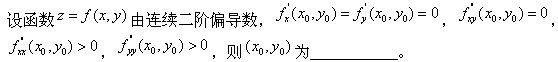
-
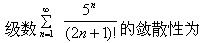
-
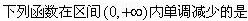
-
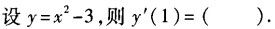
-
设两个互相独立的随机变量X和Y的方差分别为2和4,则随机变量2X-3Y的方差;是()。
-
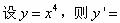
-

-
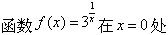
-

-
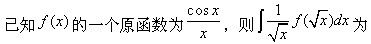
-
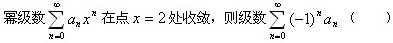
-
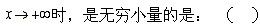
-
将一枚硬币重复掷n次,以X和Y分别表示正面向上和反面向上的次数,则X与Y的相关系数等于()。
-

-
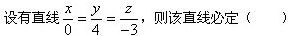
-
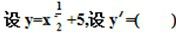
-
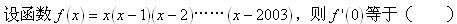
-
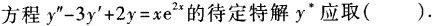
-
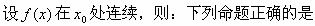
-
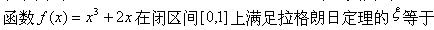
-
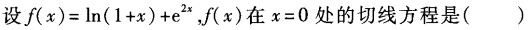
-
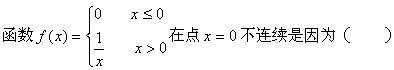
-
下列矩阵中A与B合同的是()。
-
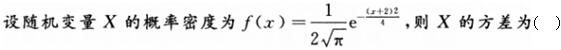
-
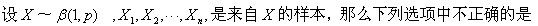
-
下列式子中成立的是
-

-
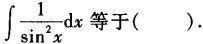
-
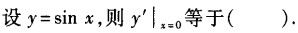
-
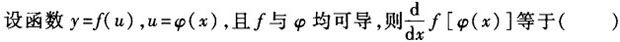
-
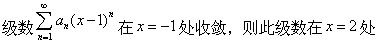
-
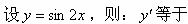
-
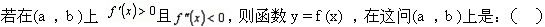
-
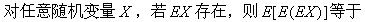
-
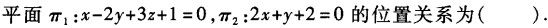
-

-
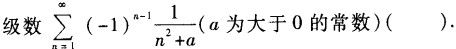
-
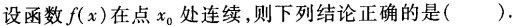
-
-
下列n阶行列式,一定等于-1的是()。
-
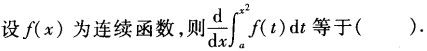
-
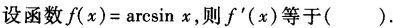
-
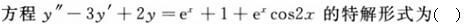
-
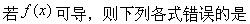
-
在假设检验问题中,犯第一类错误的概率α的意义是()
-

-
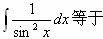
-
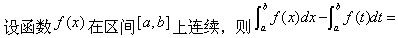
-
下列微分方程中,一阶线性齐次方程是
-
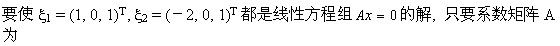
-
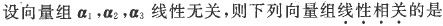
-
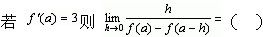
-
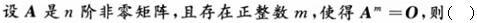
-
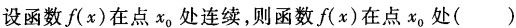
-
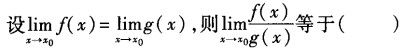
-
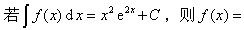
-
-

-
-
-
在对单个正态总体均值的假设检验中,当总体方差已知时,选用()
-
-
-
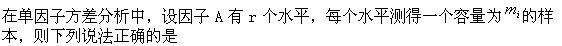
-
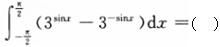
-
-
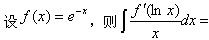
-
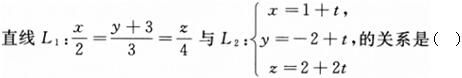
-
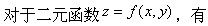
-
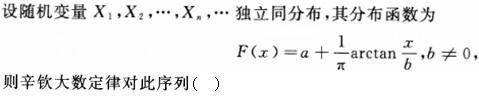
-
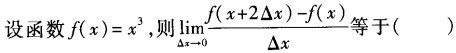
-
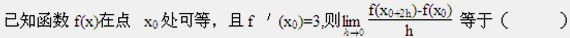
-
-
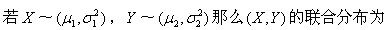
-
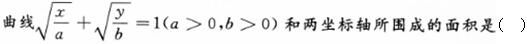
-
设f(x)为区间[a,b]上的连续函数,则曲线y=f(x)与直线x=a,x=b,y=0所围成的封闭图形的面积为().
-
设y=f(x)在(a,6)内有二阶导数,且,f″>0,则曲线y=f(x)在(a,6)内().
-
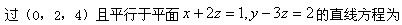
-
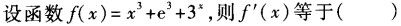
-
若向量组α,β,γ线性无关,α,β,σ线性相关,则()。
-
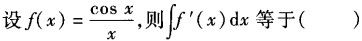
-
-
-
-

-
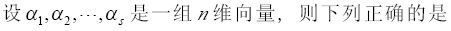
-
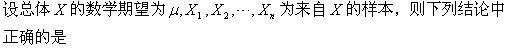
-

-
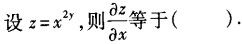
-
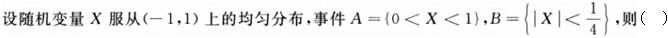
-
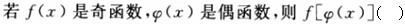
-
设随机事件A与B相互独立,且P(B)=0.5,P(A-B)=0.3,则P(B-A)=()。
-

-
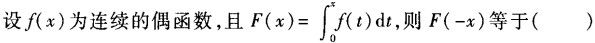
-
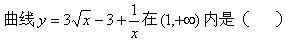
-
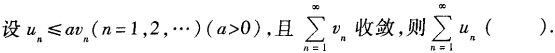
-

-
从1、2、3、4、5这五个数字中等可能地、有放回地接连抽取两个数字,则这两个数字不相同的概率为()
-
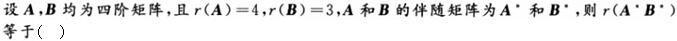
-
-
-
-
-
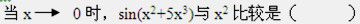
-

-
下列命题正确的是().
-
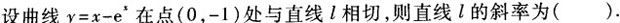
-
设随机变量X服从指数分布,则随机变量Y=min(X,2)的分布函数()。
-
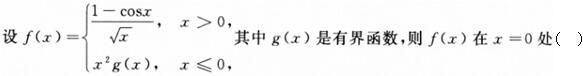
-
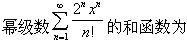
-
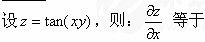
-
投掷两个均匀的骰子,已知点数之和是偶数,则点数之和为6的概率为()
-
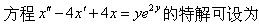
-

-
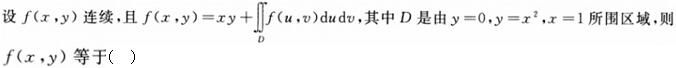
-
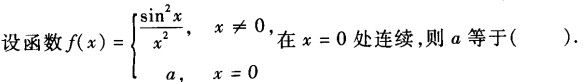
-
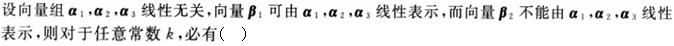
-

-
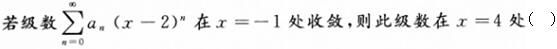
-
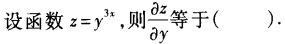
-
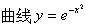
-
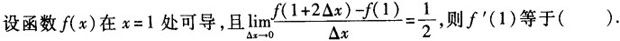
-
已知二维随机变量(X,Y)服从区域[0,1]×[0,1]上的均匀分布,则()。
-
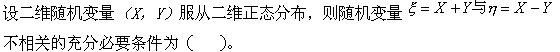
-
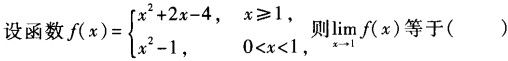
-
下列积分不为0的是
-
设4阶矩阵A与B仅有第3行不同,且|A|=1,|B|=2,则|A+B|=()。
-
下列广义积分收敛的是
-
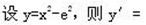
-
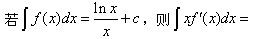
-
-

-
-

-
-
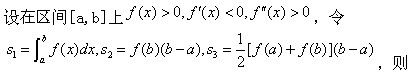
-
-
-

-

-
-
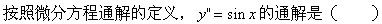
-
-
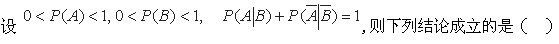
-
-
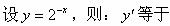
-
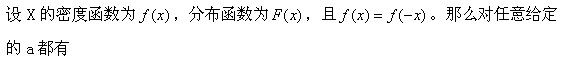
-
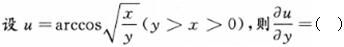
-
假设随机变量X的分布函数为F(x),密度函数为f(x).若X与-X有相同的分布函数,则下列各式中正确的是()
-

-
若事件A与B为互斥事件,且P(A)=0.3,P(A+B)=0.8,则P(B)等于().
-
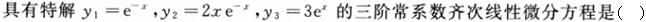
-
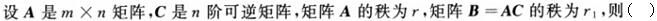
-
-
-
-
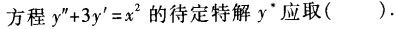
-

-
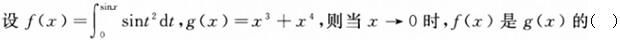
-
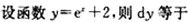
-
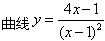
-
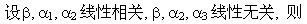
-
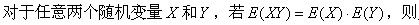
-
-
-
当事件A与事件B同时发生时,事件C必发生,则()。
-
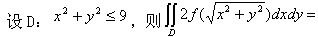
-
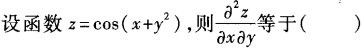
-
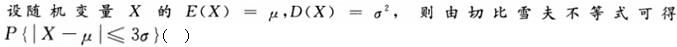
-
下列命题中正确的有().
-
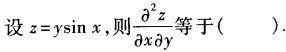
-
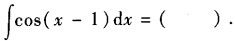
-
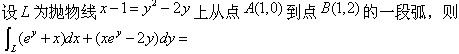
-

-
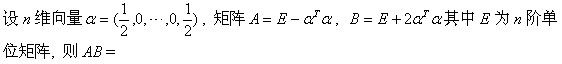
-
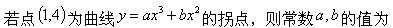
-
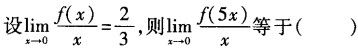
-
以下结论正确的是().
-
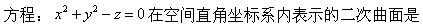
-
设A、B都是n阶非零矩阵,且AB=0,则A和B的秩
-
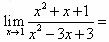
-
设在f(x)上连续,在[0,1]内可导,且f(0)=f(1),则:在(0,1)内曲线y=f(x)的所有切线中
-
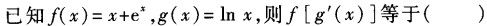
-
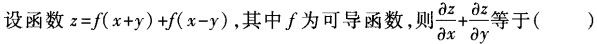
-
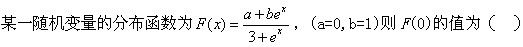
-
在一次军事演习中,某舟桥连接到命令要赶到某小河D岸为进行中的A部队架设浮桥。假设舟桥连到达D岸的时间服从7点到7点30分这时间段内的均匀分布,架设需要20分钟时间,A部队到达D岸的时间服从7点30分到8点这时间段内的均匀分布。且舟桥连的到达时间和A部队的到达时间相互独立。则A部队到达D岸时能立即过桥的概率是()。
-
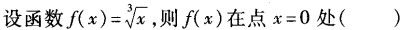
-

-
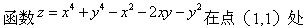
-
若f(-x)=f(x),且在(0,+∞)内f′(x)>0,f″(x)<0,则f(x)在(-∞,0)内()。
-
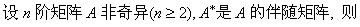
-
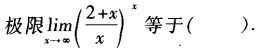
-
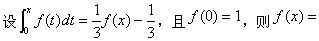
-
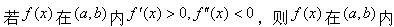
-

-
零为矩阵A的特征值是A为不可逆的
-
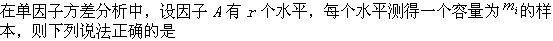
-
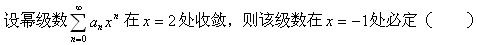
-
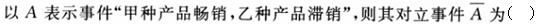
-
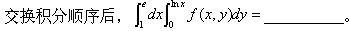
-

-
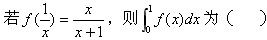
-

-
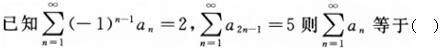
-
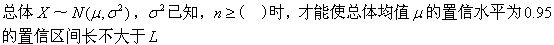
-
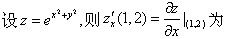
-
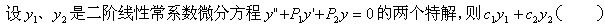
-
当x→0时,3x是x的().
-
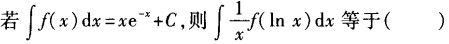
-
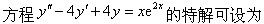
-
下列各对函数中相同的是:
-
设函数f(x)在区间(0,1)内可导,f′(x)>0,则在(0,1)内f(x)().
-
在一次假设检验中,下列说法正确的是
-
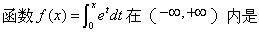
-
设2n阶行列式D的某一列元素及其余子式都等于a,则D=()。
-
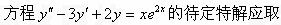
-

-
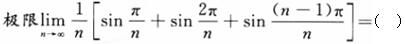
-
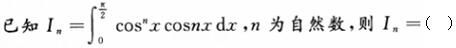
-
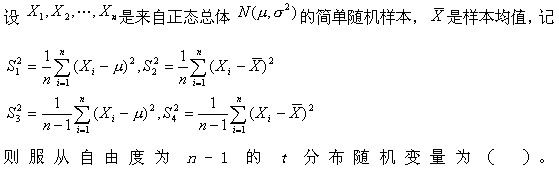
-
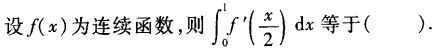
-

-
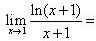
-
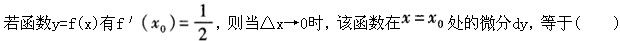
-
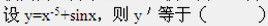
-

-

-
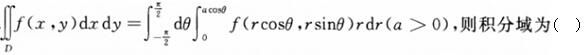
-

-
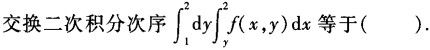
-
下面哪个函数在其定义域内不连续()。
-
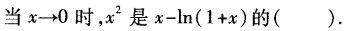
-

-
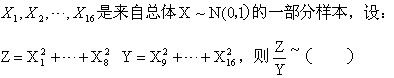
-
函数y=f(x)满足f(1)=2,f″(1)=0,且当x<1时,f″(x)<0;当x>l时,f″(x)>O,则有().
-
当x→2时,下列函数中不是无穷小量的是().
-
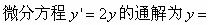
-

-
-
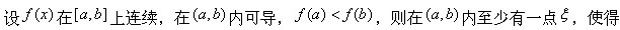
-
下列定积分的值等于0的是().
-
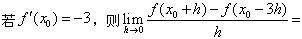
-
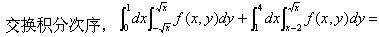
-

-
设y=sin2x,则y′等于().
-
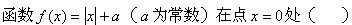
-
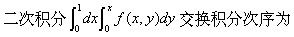
-
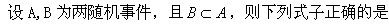
-
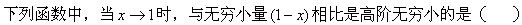
-
设某宿舍共有5名士兵,就寝时帽子均统一挂在宿舍内的帽钩上,在连队进行夜间紧急集合训练时,该宿舍的5名士兵随机从帽钩上拿一顶帽子戴上,则正好戴的是自己帽子的平均战士人数为()。
-
下列矩阵中不能相似对角化的为()。
-
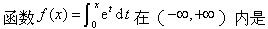
-
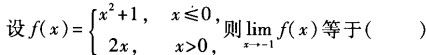
-
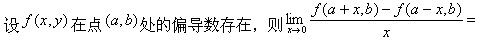
-
在下列级数中,条件收敛的是
-
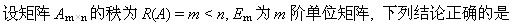
-
下列矩阵为正定的是
-
下列定积分中,其值为零的是()
-
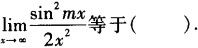
-
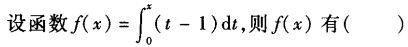
-
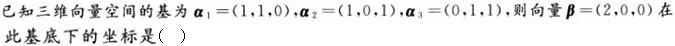
-
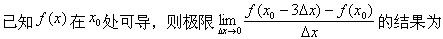
-
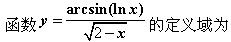
-
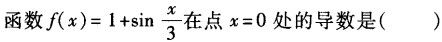
-
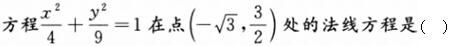
-
设A、B都是n阶方阵,下面结论正确的是
-
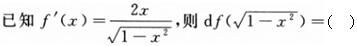
-
下列关系正确的是().
-
袋中有50个乒乓球,其中20个黄的,30个白的,现在两个人不放回地依次从袋中随机各取一球。则第二人取到黄球的概率是()
-
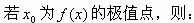
-

-
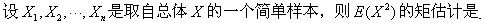
-
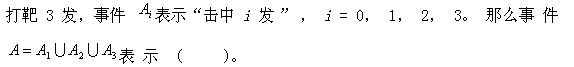
-

-
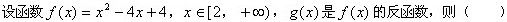
-
若a·b=a·c,则()。
-
设A、B为同阶可逆矩阵,则
-
下列级数收敛的是
-
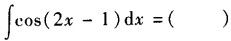
-
在手机号码中,后8位不出现“8”的概率为()。
-
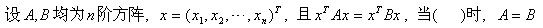
-
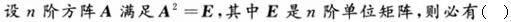
-
同时抛掷三枚质地完全相同的硬币,则正面与反面都出现的概率为()。
-
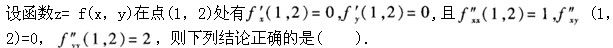
-

-
下列矩阵中,()不是初等矩阵。
-
若事件A发生必然导致事件B发生,则事件A和B的关系一定是().
-
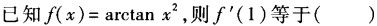
-
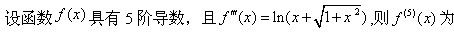
-
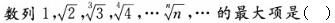
-
下列反常积分发散的是()。
-
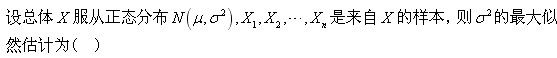
-
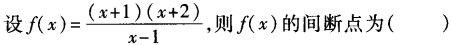
-
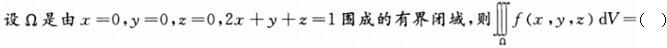
-

-
设100件产品中有次品4件,从中任取5件的不可能事件是().
-
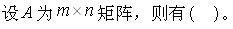
-
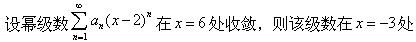
-
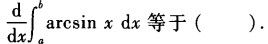
-
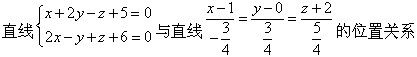
-
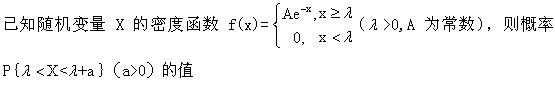
-
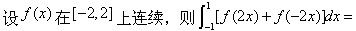
-
设A为m×n矩阵,齐次线性方程组Ax=0仅有零解的充要条件是()。
-
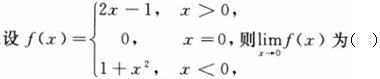
-
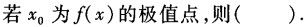
-
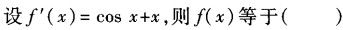
-
下列二无函数中,()可以作为连续型随机变量的联合概率密度。
-
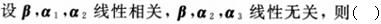
-
战士甲进行射击训练,已知甲每次射击击中10环、9环、8环或8环以下的概率分别为0.2,0.3,0.5。现甲独立射击了2次,则甲至少有1次射中10环的概率是()。
-
已知随机变量X与Y有相同的且不为零的方差,则X与Y相关系数ρ=1的充分条件是()。
-
-
-
-
当x→0时,下列结论正确的是
-
设A是n阶方阵,则|A|=0的必要条件是().
-
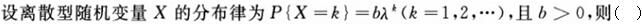
-
设A为m×n矩阵,C是n阶可逆矩阵,矩阵A的秩为r1,矩阵B=AC的秩为r,则
-
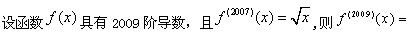
-
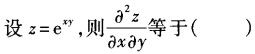
-
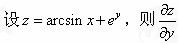
-
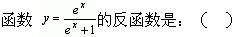
-
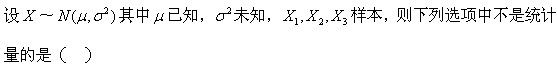
-
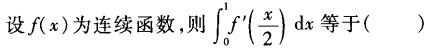
-
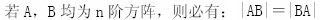
-
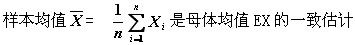
-
设AB为门阶方阵,若AB等价,则AB相似
-
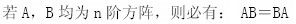
-

-

-
设A、B是Ω中的随机事件,则(A∪B)-B=A
-

-
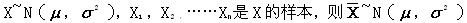
-
齐次线性方程组AX=0若有两个不同的解,它就有无穷多个解
-
假设检验基本思想的依据是小概率事件原理
-
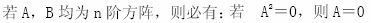
-
若A是实对称矩阵,则A的特征值全为实数
-
设方阵A满足AA=A,则必有A=O或A=E
-
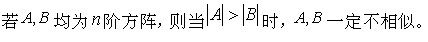
-
若A是m×n矩阵,且m≠n,则当R(A)=m时,非齐次线性方程组AX=b,有解
-
若A是m×n矩阵,且m≠n,则当R(A)=n时,齐次线性方程组AX=0只有零解
-
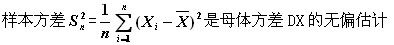
-
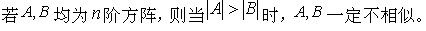
-
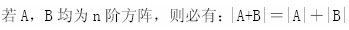
-
若A是实对称矩阵,则A为正定矩阵的充要条件是A的特征值全为正
-
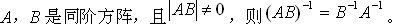
-
对任意事件A与B,则有P(A∪B)=P(A)+P(B)
-

-
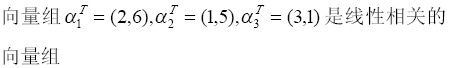
-
对任意事件A和B,必有P(AB)=P(A)P(B)
-
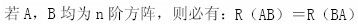
-

-
若A是m×n矩阵,且m≠n,则当A的列向量组线性无关时,A的行向量组也线性无关
-
设A,B是不可逆的同阶方阵,则|A|=|B|
-
若A是实对称矩阵,则若|A|>O,则A为正定的
-
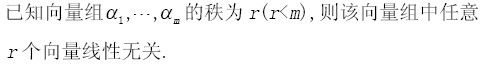
-
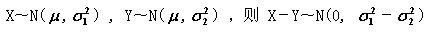
-
若X服从二项分布b(k;n,p),则EX=npq
-

-
方阵A可逆的充分必要条件是A的特征值不全为零
-
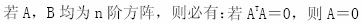
-
X为随机变量,则DX=Cov(X,X)
-
设A、B是Ω中的随机事件,必有P(A-B)=P(A)-P(B)
-
若A是m×n矩阵,且m≠n,则当R(A)=n时,非齐次线性方程组AX=b,有唯一解
-
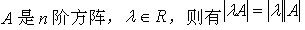
-
设A、B是Ω中的随机事件,则A∪B=A∪AB∪B
-
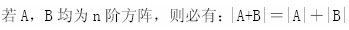
-
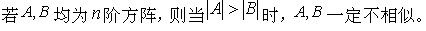
-
对任意事件A与B,则有P(A∪B)=P(A)+P(B)
-
对称矩阵A正定的充分必要条件是|A|>O
-
若X服从参数为λ的普哇松分布,则EX=DX
-
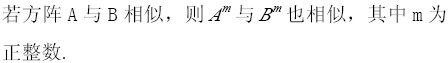
-
若X服从二项分布b(k;n,p),则EX=p
-
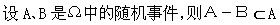
-
若A是实对称矩阵,则A的特征值全为实数
-
若A是m×n矩阵,且m≠n,则当R(A)=n时,非齐次线性方程组AX=b,有唯一解
-
若A是实对称矩阵,则若|A|>O,则A为正定的
-

-
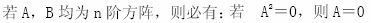
-
若A是实对称矩阵,则A为正定矩阵的充要条件是A的特征值全为正
-
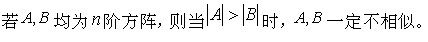
-

-
若A是m×n矩阵,且m≠n,则当R(A)=m时,非齐次线性方程组AX=b,有解
-
齐次线性方程组AX=0若有两个不同的解,它就有无穷多个解
-
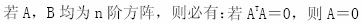
-

-
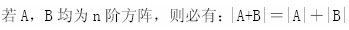
-
对称矩阵A正定的充分必要条件是|A|>O
-
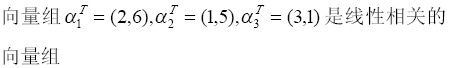
-
设AB为门阶方阵,若AB等价,则AB相似
-
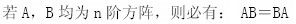
-
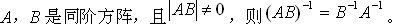
-
若A是m×n矩阵,且m≠n,则当A的列向量组线性无关时,A的行向量组也线性无关
-
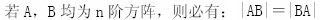
-

-
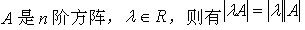
-
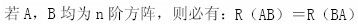
-
设方阵A满足AA=A,则必有A=O或A=E
-
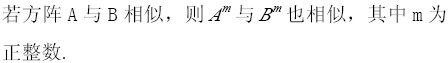
-

-
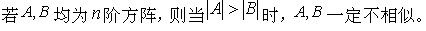
-
方阵A可逆的充分必要条件是A的特征值不全为零
-
设A,B是不可逆的同阶方阵,则|A|=|B|
-

-
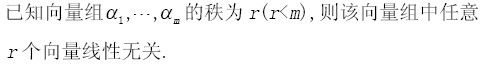
-
若A是m×n矩阵,且m≠n,则当R(A)=n时,齐次线性方程组AX=0只有零解
-
对任意事件A与B,则有P(A∪B)=P(A)+P(B)
-
X为随机变量,则DX=Cov(X,X)
-
若X服从参数为λ的普哇松分布,则EX=DX
-
设A、B是Ω中的随机事件,则(A∪B)-B=A
-
设A、B是Ω中的随机事件,必有P(A-B)=P(A)-P(B)
-
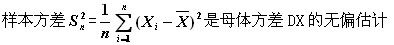
-
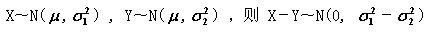
-
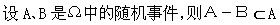
-
对任意事件A与B,则有P(A∪B)=P(A)+P(B)
-
X为随机变量,则DX=Cov(X,X)
-
若X服从参数为λ的普哇松分布,则EX=DX
-
设A、B是Ω中的随机事件,则(A∪B)-B=A
-
设A、B是Ω中的随机事件,必有P(A-B)=P(A)-P(B)
-
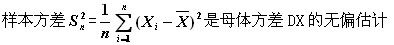
-
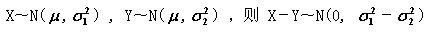
-
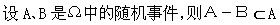
 Copyright 2023 上海欣师教育科技有限公司
Copyright 2023 上海欣师教育科技有限公司